Quantum Computing Research

About Us

Quantum computing harnesses many unique properties of quantum mechanics, such as quantum entanglement and superposition, offering distinct capabilities that exceed those of conventional computing apparatus. Our overarching objective is to devise efficient quantum algorithms tailored to address scientific computational issues, particularly those that present formidable challenges to classical computers.

Our Research

Hamiltonian Simulations

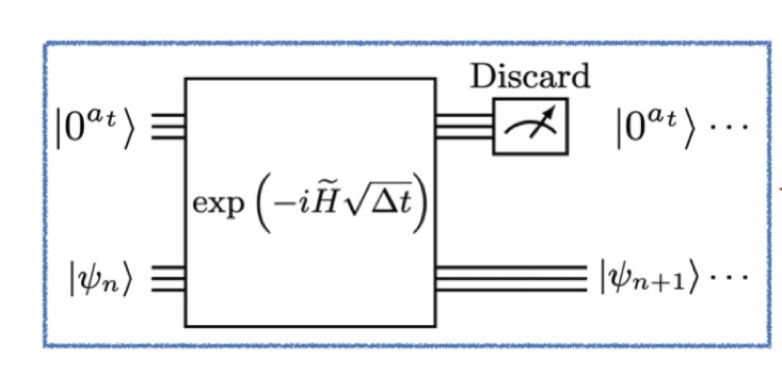
Hamiltonian simulation algorithms involve constructing a quantum circuit that performs the unitary transformation U associated with a Hamiltonian operator H. They are important building blocks for many other quantum computing algorithms.

Open Quantum Systems

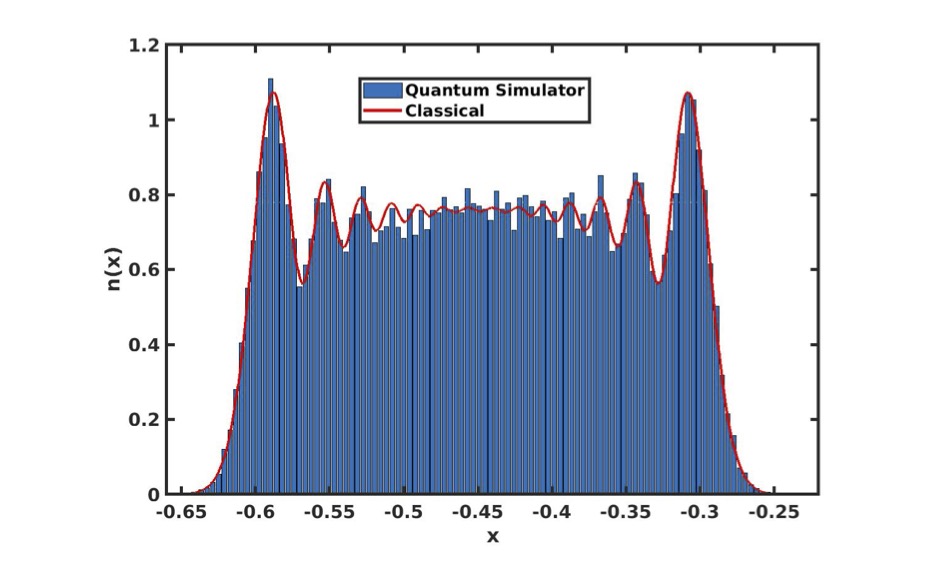
In practice, quantum systems are inevitably subject to environmental noise. We design both quantum and classical algorithms to effectively simulate the behavior of these open quantum systems.

Applications to Material Science

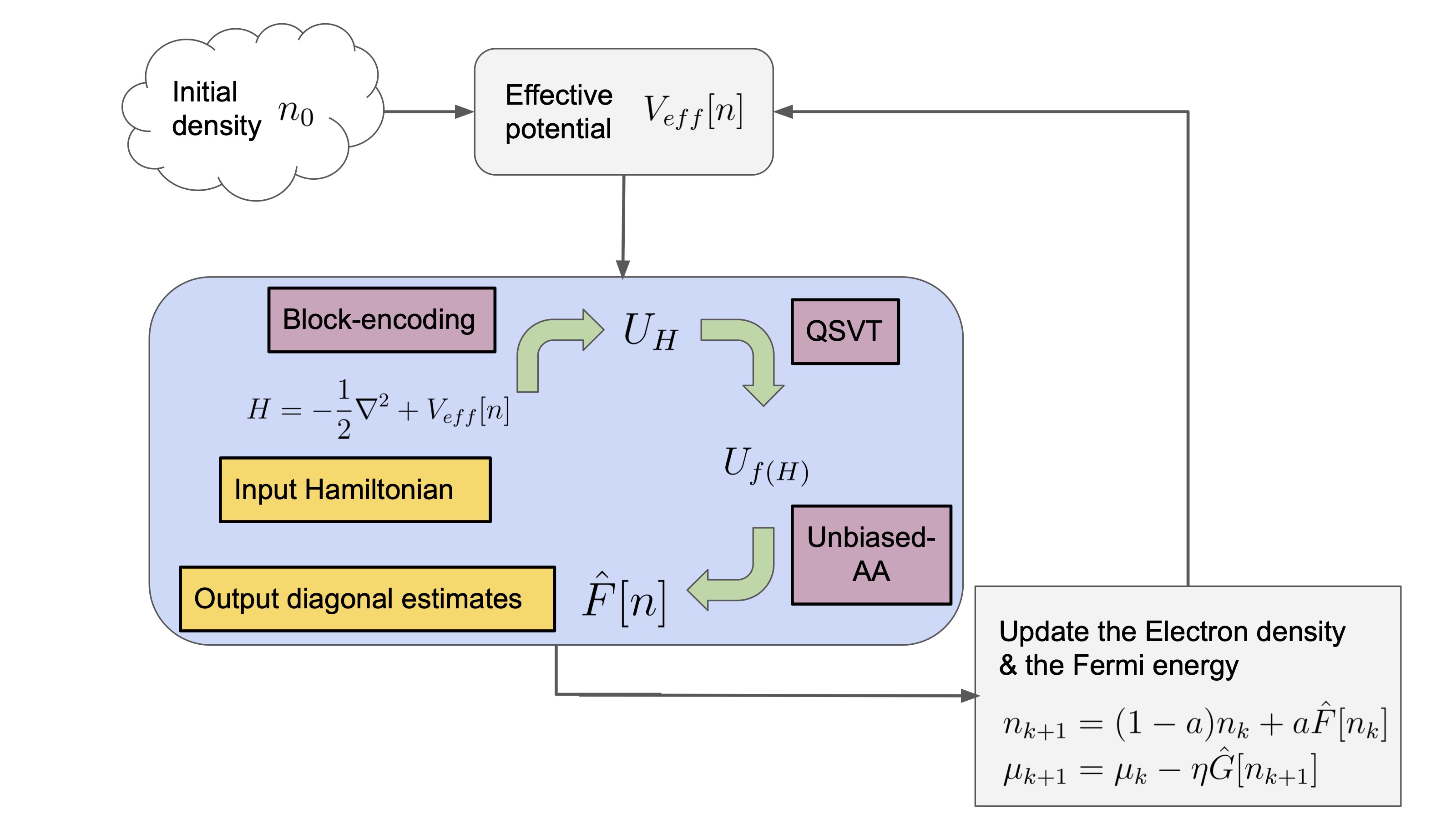
First-principle calculations in material science eliminate the need for empirical assumptions and possess the potential to predict material properties with quantum-level precision.

Quantum Algorithms for PDEs

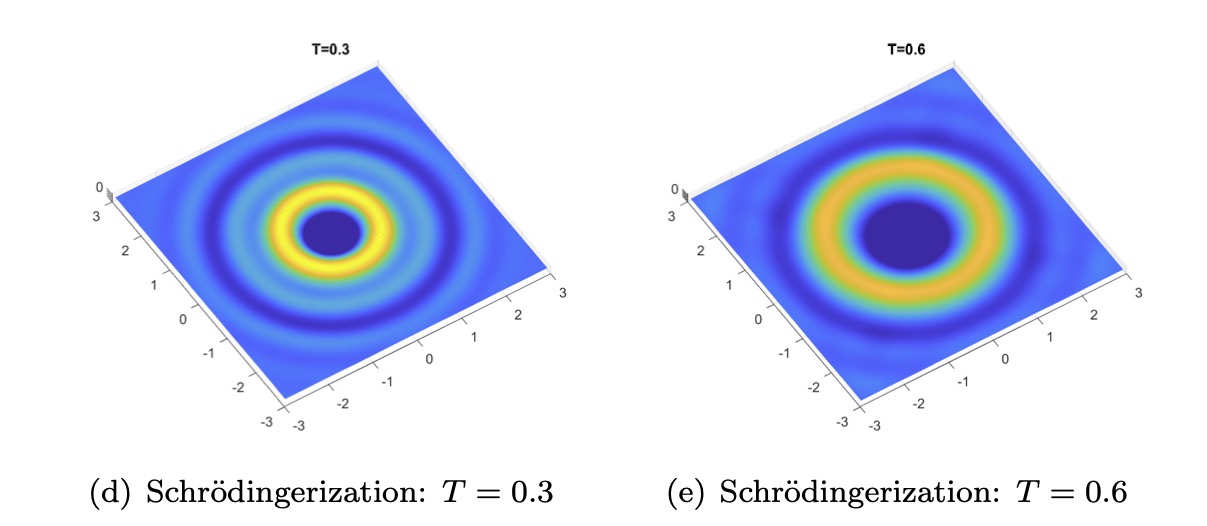
We create quantum algorithms specifically designed to solve partial differential equations, particularly in situations where the numerical discretization results in a high degree of freedom.

Learning Open Quantum Systems

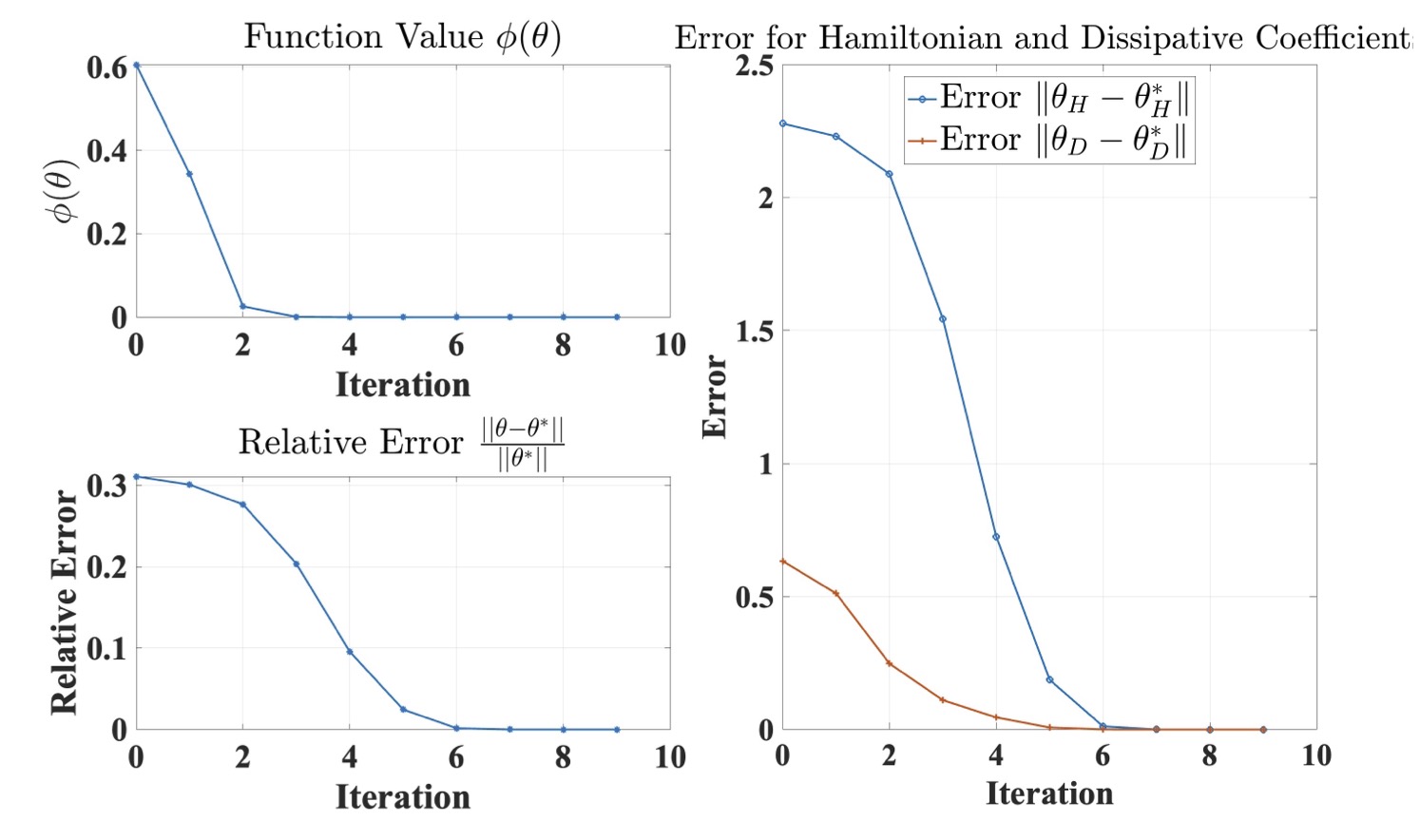
Using measurement data, these learning algorithms are designed to infer the interactions in a quantum system, which can then be leveraged to control quantum dynamics or implement quantum algorithms.

Quantum Algorithms for Statistical Sampling

Quantum algorithms speed up Markov Chain Monte Carlo by leveraging quantum walks to reduce mixing time, using quantum amplitude amplification to improve sampling efficiency, and exploiting quantum search techniques to accelerate convergence.

Publications

1. Ke Wang and Xiantao Li, Non-Markovian Noise Mitigation: Practical Implementation, Error Analysis, and the Role of Environment Spectral Properties, preprint, 2025.
2. Zhenning Liu, Xiantao Li, Chunhao Wang, and Jin-Peng Liu Toward end-to-end quantum simulation for protein dynamics, preprint, 2024.
3. Hsuan-Cheng Wu and Xiantao Li, Structure-preserving quantum algorithms for linear and nonlinear Hamiltonian systems, preprint, 2024.
4. Hsuan-Cheng Wu, Jiayao Wang and Xiantao Li, Quantum Algorithms for Nonlinear Dynamics: Revisiting Carleman Linearization with No Dissipative Conditions, SIAM Journal on Scientific Computing, 2025.
5. Wenhao He, Tongyang Li, Xiantao Li Zecheng Li, Chunhao Wang and Ke Wang, Efficient Optimal Control of Open Quantum Systems, TQC, 2024.
6. Zhiyan Ding, Xiantao Li and Lin Lin, Simulating Open Quantum Systems Using Hamiltonian Simulations, PRX Quantum, 5, 020332, 2024.
7. Zhiyan Ding, Taehee Ko, Jiahao Yao, Lin Lin, and Xiantao Li, Random coordinate descent: a simple alternative for optimizing parameterized quantum circuits, Physical Review Research, 2024.
8. Guneykan Ozgul, Xiantao Li, Mehrdad Mahdavi, Chunhao Wang, Stochastic Quantum Sampling for Non-Logconcave Distributions and Estimating Partition Functions, ICML, 2024.
9. With Taehee Ko and Chunhao Wang, Implementation of the Density-functional Theory on Quantum Computers with Linear Scaling with respect to the Number of Atoms, QEC. 2024
10. With Ke Wang, Simulation-assisted learning of open quantum systems, Quantum, 2024.
11. With Jin, Liu, Yu, Quantum Simulation for Partial Differential Equations with Physical Boundary or Interface Conditions., Journal of Computational Physics, Vol 498, 112707, 2024.
12. With Jin, Liu, Yu, Quantum Simulation for Quantum Dynamics with Artificial Boundary Condition, SIAM Journal on Scientific Computing, 2024.
13. With C. Wang, Efficient Quantum Algorithms for Quantum Optimal Control, Proceedings of the 40th International Conference on Machine Learning (ICML), 2023.
14. With C. Wang, Efficient Simulating Markovian open quantum systems using higher-order series expansion, 50th International Colloquium on Automata, Languages, and Programming (ICALP), 2023.
15. Enabling Quantum Speedup of Markov Chains using a Multi-level Approach, Preprint, 2022.
16. With S. Jin and Nana Liu, Hamiltonian Simulation in the semi-classical regime Quantum, Vol 6, pp 739, 2022.
17. X Li, Some Error Analysis for the Quantum Phase Estimation Algorithms Journal of Physics A: Mathematical and Theoretical, 2022.
18. With Chunhao Wang, Succinct Description and Efficient Simulation of Non-Markovian Open Quantum Systems Communications in Mathematical Physics, Vol 401, pages 147–183, 2023.
19. With Shi Jin, A Partially Random Trotter Algorithm for Quantum Hamiltonian Simulations, Communications on Applied Mathematics and Computation, 2023.

Our Team